반응형
백준 1707번 문제 - 이분 그래프
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에
www.acmicpc.net
문제 분석
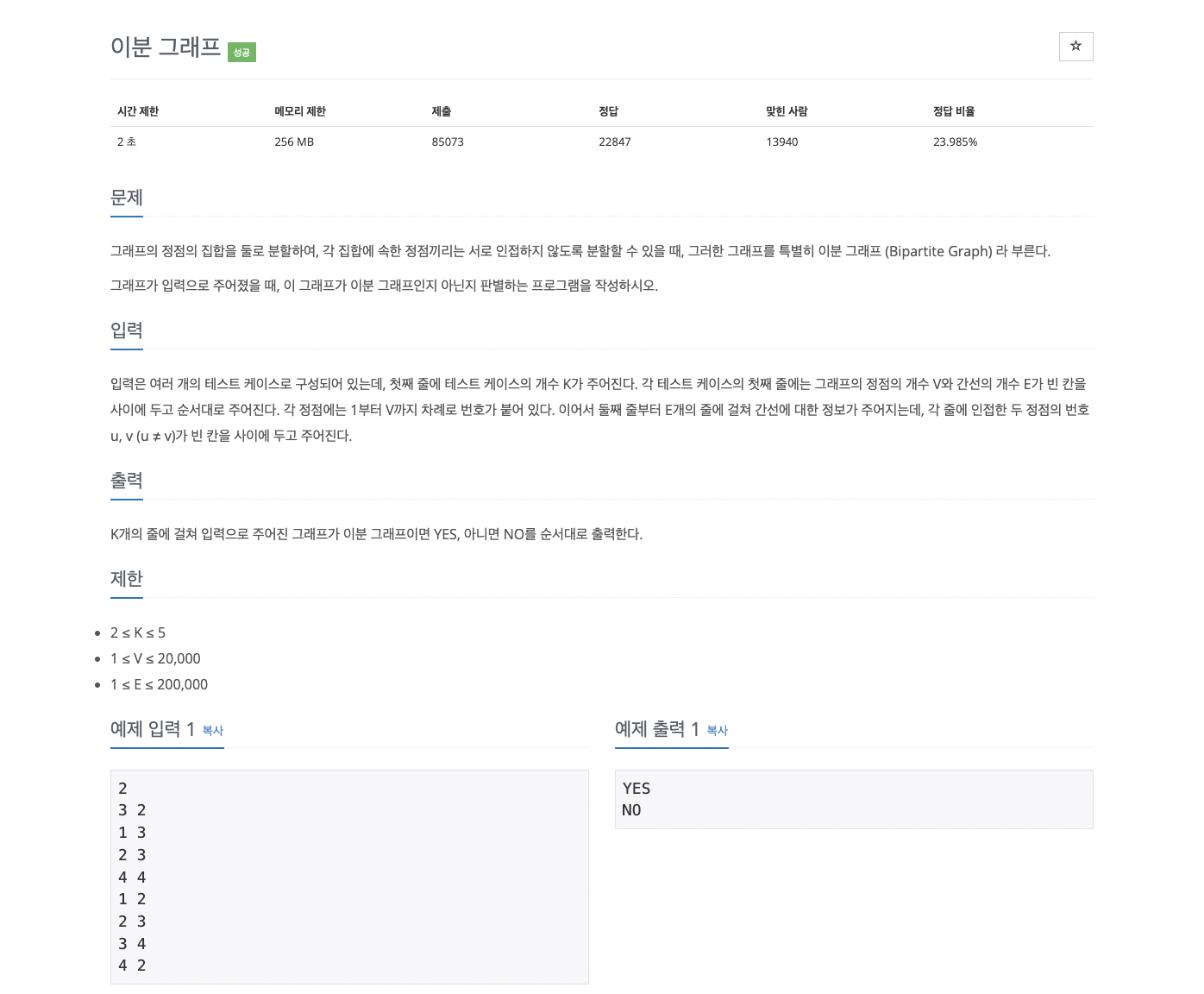
- 몇 번 동작할지(K) 입력 → 정점(V), 간선(E) 입력 → 간선 입력 → 이분 그래프가 가능하면 YES, 아니면 NO 출력
해결 키 포인트
- BFS(너비 우선 탐색) 개념 파악
- 이분 그래프 개념 파악
- 해당 정점과 연결된 정점은 다른 그룹, 인접 리스트 중에 값은 그룹이 존재 하지 않는 그래프
- (사이클이 존재할 때 홀수 사이클이면 이분 그래프 아님)
너비 우선 탐색(BFS)
그래프 완전 탐색 기번 중 하나로, 그래프의 시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다.
너비 우선 탐색의 핵심 이론
- 한번 방문한 노드를 다시 방문하면 안되므로 노드 방문 여부를 체크할 배열이 필요
- 그래프는 인접 리스트로 표현
- DFS의 탐색 방식은 선입 선출 특성을 가짐 ( 큐 사용 )
알고리즘
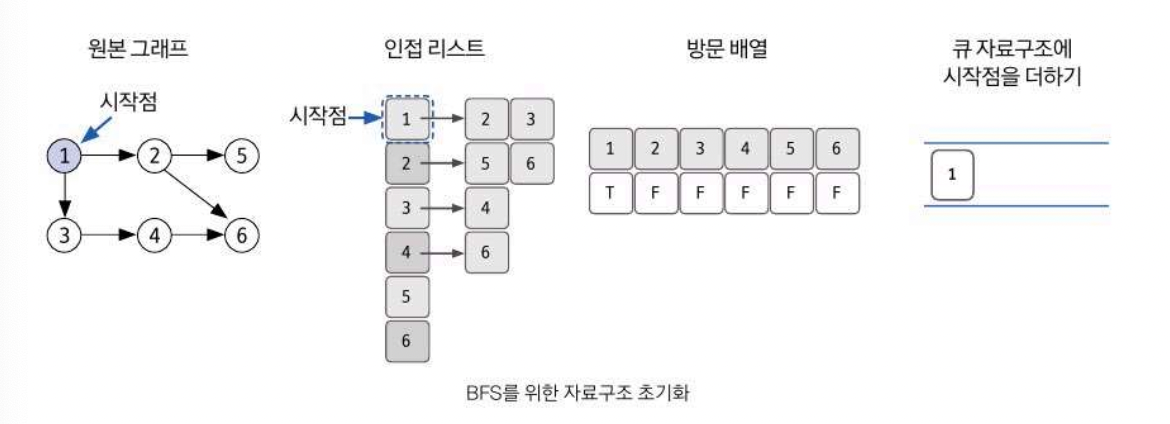
1. BFS를 시작할 노드를 정한 후 사용할 자료구조 초기화
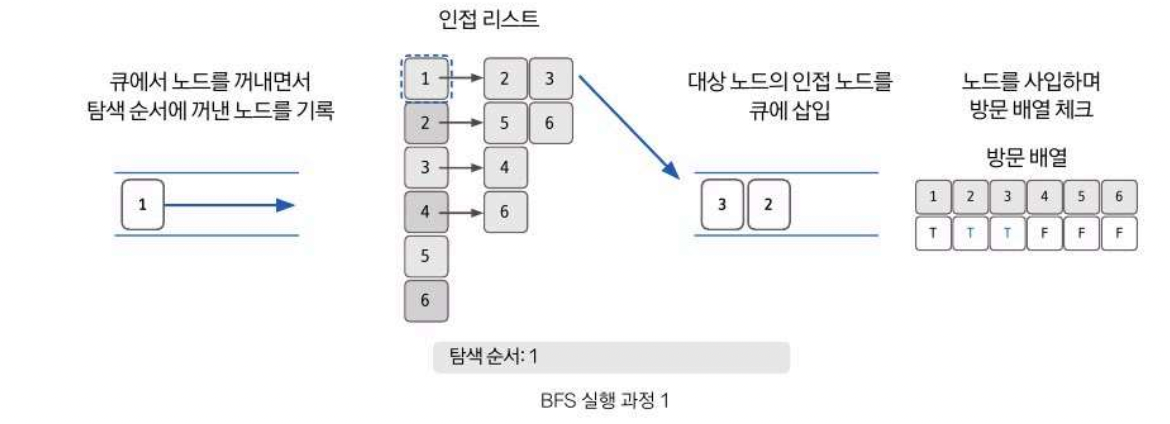
2. 큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입 (이를 모든 정점에 다한다)
만약 큐에 노드가 없으면, 방문하지 않은 정점을 알아내, 큐에 삽입하고 다시 2번 단계를 반복한다.
코드
import java.io.*;
import java.util.*;
public class Main {
static ArrayList<Integer> [] lists;
static boolean [] isChecked;
static int [] bipartiteGraph;
static boolean isBipartiteGraph;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// K 입력
int K = Integer.parseInt(br.readLine());
for (int i = 0; i < K; i++) {
// 정점 개수(V), 간선 개수(E) 입력
StringTokenizer st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
// 변수 초기화
isBipartiteGraph = true;
isChecked = new boolean[V];
bipartiteGraph = new int[V];
lists = new ArrayList[V];
for(int j=0;j<V;j++) {
lists[j] = new ArrayList<>();
}
// 간선 입력
for(int j=0;j<E;j++) {
st = new StringTokenizer(br.readLine());
int s = Integer.parseInt(st.nextToken())-1;
int e = Integer.parseInt(st.nextToken())-1;
lists[s].add(e);
lists[e].add(s);
}
// bfs 실행
for(int j=0;j<V;j++) {
if(!isChecked[j])
bfs(j);
// 벌써 이분 그래프가 불가능 할 경우, 그만 확인
if(!isBipartiteGraph)
break;
}
// 이분 그래프가 가능할 경우, YES
// 아닐 경우, NO
if(isBipartiteGraph)
bw.write("YES\n");
else
bw.write("NO \n");
}
bw.flush();
bw.close();
}
public static void bfs (int index) {
Queue<Integer> queue = new LinkedList<>();
queue.add(index);
bipartiteGraph[index] = 0;
isChecked[index] = true;
// 이분 그래프가 안되거나, 큐에 값이 존재하지 않을 때까지 반복
while(!queue.isEmpty() && isBipartiteGraph) {
// 현재 queue에서 하나 뽑아 해당 index(now) 인접 정점 값 중 확인 하지 않은 값은 queue에 추가
int now = queue.poll();
for(int i=0;i<lists[now].size();i++) {
// index(now)의 i번째 인접 정점 값
int newIndex = lists[now].get(i);
// 체크 안된것만 확인
if(!isChecked[newIndex]) {
// 이분 그래프가 잘 작동하는지 알기 위한 배열 (0 또는 1의 값으로, 0끼리 한 묶음 | 1끼리 한 묶음)
// 현재 값(newIndex)은 파생 전(now) 값과 다른 값으로
bipartiteGraph[newIndex] = (bipartiteGraph[now] + 1) % 2;
// 현재 값에 인접 리스트에서 같은 묶음인 경우가 존재하는지 확인
// 존재할 경우는 이분 그래프 불가능하므로 isBipartiteGraph를 false로
for(int j=0;j<lists[newIndex].size();j++) {
int check = lists[newIndex].get(j);
if(isChecked[check] && bipartiteGraph[check] == bipartiteGraph[newIndex] )
isBipartiteGraph = false;
}
// 체크 됐으니 배열 true로, 큐에 추가
isChecked[newIndex] = true;
queue.add(newIndex);
}
}
}
}
}반응형
'CodingTEST' 카테고리의 다른 글
| [백준 1717] 집합의 표현 (JAVA) (2) | 2023.08.26 |
|---|---|
| [백준 2251] 물통 (JAVA) (0) | 2023.08.25 |
| [백준 1325] 효율적인 해킹 (JAVA) (0) | 2023.08.23 |
| [백준 18352] 특정 거리의 도시 찾기 (JAVA) (0) | 2023.08.21 |
| [백준 1033] 칵테일 (JAVA) (0) | 2023.08.17 |



